Số thực là gì?

Số thực là gì, tụ tập số thực bao gồm những số nào? Mời chúng ta gọi nội dung bài viết sau đây nhằm làm rõ rộng lớn về kỹ năng và kiến thức toán học tập cần thiết này nhé.

1. Số thực là gì?

Số thực là tụ tập số hữu tỉ và số vô tỉ.
Tập hợp $\mathbb{R}$ là ký hiệu của tụ tập số thực, bao gồm những số thực.

$\mathbb{R = Q \cup}I$

Tập số thực $\mathbb{R}$ phủ kín trục số.

Ví dụ: $1;\frac{1}{2}; - 1.254, - 3\frac{1}{4},\sqrt{5},....$

2. Trục số thực

Mỗi số thực được màn trình diễn bởi vì một điểm bên trên trục số.

Ngược lại từng điểm bên trên trục số đều màn trình diễn một trong những thực.
Chỉ sở hữu tụ tập số thực mới mẻ lấp giàn giụa trục số.

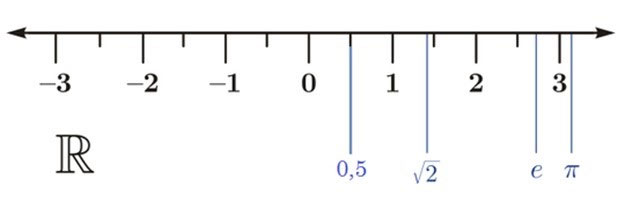
3. So sánh những số thực

Phương pháp

Với nhị số thực x, nó bất kì, tớ luôn luôn sở hữu x = nó hoặc x < nó hoặc x > y
Các số thực to hơn 0 gọi là số thực dương, những số thực nhỏ rộng lớn 1 gọi là những số thực âm. Số 0 ko là số thực dương cũng ko là số thực âm
Việc đối chiếu những số thực dương thực hiện tương tự động như đối chiếu những số hữu tỉ
Với a, b là nhị số thực dương, nếu như a > b thì $\sqrt{a} > \sqrt{b}$ .

Ví dụ: Điền một chữ số phù hợp vô vị trí vuông:

a) -7,5(...)8 > -7,513	b) -3,02 < -3,(...)1
c) -0,4(...)854 < -0,49826	d) -1,(...)0765 < -1,892

Hướng dẫn giải

a) -7,5(0)8 > -7,513

b) -3,02 < -3,(0)1

c) -0,4(9)854 < -0,49826

d) -1,(9)0765 < -1,892

Ví dụ: Sắp xếp những số thực: theo đòi trật tự kể từ nhỏ cho tới lớn

Hướng dẫn giải

Sắp xếp những số thực theo đòi trật tự kể từ nhỏ cho tới lớn:

Ví dụ: Chứng minh rằng:

Với a, b là nhị số thực dương nếu như a > b thì $a^{2} > b^{2}$

Hướng dẫn giải

Nếu a > b thì $a^{2} > b^{2}$

a, b là nhị số thực dương nên a + b > 0

Nếu a > b thì a – b > 0

Xét tích

Vì nên hoặc a² – b² > 0

=> a² > b² => dpcm

3. Tính hóa học của tập luyện số thực

Trong tụ tập $\mathbb{R}$ , tớ cũng khái niệm những quy tắc toán nằm trong trừ, nhân, phân chia, lũy quá, căn bậc…Và trong những quy tắc toán những số thực cũng đều có những đặc điểm tựa như các quy tắc toán vô tụ tập những số hữu tỉ.

Trong tụ tập những số thực, những quy tắc tính sở hữu những đặc điểm so với quy tắc nhân như sau:

- Tức là với những quy tắc tính bên trên $\mathbb{R}$ cũng đều có những đặc điểm giao phó hoán, phối kết hợp như bên trên những tập luyện số không giống. Và vấn đề đó tương tự động với những quy tắc trừ, nhân, chia…

Mối mối quan hệ trong số những tập luyện số

$\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}$

Ví dụ: Thực hiện nay quy tắc tính: $\left( \frac{1}{12} - 0,32 \right):\left( 4\frac{2}{3} + 0,15 \right)$

Hướng dẫn giải

$\begin{matrix} \left( {\dfrac{1}{{12}} - 0,75} \right):\left( {4\dfrac{2}{3} + 3,5} \right) \hfill \\ = \left( {\dfrac{1}{{12}} - \dfrac{{75}}{{100}}} \right):\left( {\dfrac{{14}}{3} + \dfrac{{35}}{{10}}} \right) \hfill \\ = \left( {\dfrac{1}{{12}} - \dfrac{3}{4}} \right):\left( {\frac{{14}}{3} + \dfrac{{21}}{6}} \right) \hfill \\ = \left( {\dfrac{1}{{12}} - \dfrac{9}{{12}}} \right):\left( {\dfrac{{28}}{6} + \dfrac{{21}}{6}} \right) \hfill \\ = \dfrac{{ - 8}}{{12}}.\dfrac{6}{{49}} = \dfrac{{ - 4}}{{49}} \hfill \\ \end{matrix}$

Ví dụ: Tìm x, biết: $\left( 1\frac{3}{7} - x \right).3\frac{1}{3} = - 2\frac{31}{42}$

Hướng dẫn giải

$\begin{matrix} \left( {1\dfrac{3}{7} - x} \right).3\dfrac{1}{3} = - 2\dfrac{{31}}{{42}} \hfill \\ 1\dfrac{3}{7} - x = - 2\dfrac{{31}}{{42}}:3\dfrac{1}{3} \hfill \\ 1\dfrac{3}{7} - x = \dfrac{{ - 23}}{{28}} \hfill \\ x = 1\dfrac{3}{7} + \dfrac{{23}}{{28}} \hfill \\ x = 2\dfrac{1}{4} \hfill \\ \end{matrix}$

4. Giá trị vô cùng của một trong những thực

Định nghĩa: Khoảng cơ hội kể từ điểm a tới điểm 0 bên trên trục số là độ quý hiếm vô cùng của một trong những a (a là số thực). Giá trị vô cùng của số ko âm là chủ yếu nó, độ quý hiếm vô cùng của số âm là số đối của chính nó.

Tổng quát:

Tính chất

Giá trị vô cùng của từng số đều ko âm
Tổng quát: $|a| \geq 0$ với từng a ∈ R

Cụ thể:

Một vài ba tính chất

- Hai số đều nhau hoặc đối nhau thì có mức giá trị vô cùng đều nhau, và ngược lại nhị số có mức giá trị vô cùng đều nhau thì bọn chúng là nhị số đều nhau hoặc đối nhau.

Tổng quát: $|a| = |b| \Leftrightarrow \left\lbrack \begin{matrix} a = b \\ a = - b \\ \end{matrix} \right.$

- Mọi số đều to hơn hoặc bởi vì đối của độ quý hiếm vô cùng của chính nó và bên cạnh đó nhỏ rộng lớn hoặc bởi vì độ quý hiếm vô cùng của chính nó.

Tổng quát: $- |a| \leq a \leq |a|$ và $|a| = - a \Leftrightarrow a \leq 0;a = |a| \Leftrightarrow a \geq 0$

- Trong nhị số âm số nào là nhỏ hơn vậy thì có mức giá trị vô cùng rộng lớn hơn

Tổng quát: Nếu $a < b < 0 \Rightarrow |a| > |b|$

- Trong nhị số dương số nào là nhỏ hơn vậy thì có mức giá trị vô cùng nhỏ hơn

Tổng quát: Nếu $0 < a < b \Rightarrow |a| < |b|$

- Giá trị vô cùng của một tích bởi vì tích những độ quý hiếm vô cùng.

Tổng quát:

- Giá trị vô cùng của một thương bởi vì thương nhị độ quý hiếm vô cùng.

Tổng quát: $\left| \frac{a}{b} \right| = \frac{|a|}{|b|}$

5. Bài tập luyện ví dụ về số thực

Ví dụ 1: Điền lốt ∈, ∉, ⊂ phù hợp vô vị trí rỗng (…):

3 …. Q ; 3 …. R ; 3… I ; -2,53… Q;

0,2(35) …. I ; N …. Z ; I …. R.

Hướng dẫn

a) 3 ∈ Q ; 3 ∈ R ; 3 ∉ I ; -2,53 ∈ Q

b) 0,2(35) ∉ I ; N ∈ Z ; I ⊂ R

Ví dụ 2: Hãy thám thính những tập luyện hợp

a) Q ∩ I ;
b) R ∩ I.

Hướng dẫn

a) Q ∩ I = Ø ;
b) R ∩ I = I.

Ví dụ 3: Điền chữ số phù hợp vô (…)

a) – 3,02 < – 3, … 1

b) – 7,5 … 8 > – 7,513

c) – 0,4 … 854 < – 0,49826

d) -1, … 0765 < – 1,892

Hướng dẫn

a) – 3,02 < – 301
b) – 7,508 > – 7,513 ;
c) – 0,49854 < – 0,49826 ;
d) -1,90765 < – 1,892.

Ví dụ 4: Tìm x, biết:

3,2.x + (-1,2).x +2,7 = -4,9;

Hướng dẫn

3,2. x + (-1,2).x + 2,7 = -4,9

[3,2 + (-1,2)].x + 2,7 = -4,9.

2.x + 2,7 = – 4,9.

2.x = – 4,9 – 2,7

2.x = – 7,6

x = -7,6 : 2

x = -3,8

Ngoài số thực, những bạn cũng có thể thám thính hiểu thêm thắt về những khái niệm không giống vô toán học tập như số chủ yếu phương, số vô tỉ, số hữu tỉ, số yếu tố, số ngẫu nhiên...